6th International Conference Energy & Meteorology: Abstract Submission

1. Objective

As the use of solar energy spreads, the need of knowing the available solar resources at any given site or region also increases. A complete assessment of ground-level solar radiation requires knowledge of three components: direct normal irradiance (DNI), global horizontal irradiance (GHI) and diffuse horizontal irradiance (DHI). Satellite-based models can provide solar information, but must be validated and adapted before they can be confidently used, and high-quality direct, ground measurements are fundamental for such validations. Usually, GHI measurements are more widely available than DNI or DHI, with larger temporal and spatial coverages; for example, GHI has been measured across Qatar for over a decade, while DNI and DHI have been measured only in Doha, since late 2012.

If two components are known, the other can be calculated using SZA, the solar zenith angle at the time and site, with

GHI = DNI*cos(SZA) + DHI            (Eq.1)

However, since often only one component is measured, other methods must be employed. One such method is presented here.

1. Methodology

Different models have been developed to estimate DNI in locations where only either GHI or DHI is available. Most use a function relating the diffuse fraction Kd = DHI/GHI and other meteorological parameters (like temperature, humidity, sunshine hours) in order to determine DNI. A commonly used function of the diffuse fraction is its correlation with the clearness index Kt = GHI/Eth, where Eth is the radiation on a horizontal plane at the top of the atmosphere; the original model proposed by Erbs et al. [1] relates Kt and Kd at hourly level.

Here, the Erbs model is tested under arid, desert conditions, which present challenges especially due to high aerosol loads; then an approach similar to the Erbs model is used to develop a model more adequate for these regions.

1. Preliminary findings, discussion

Figure 1 shows measured one-minute Kd vs. Kt for one year, at a site in Doha, Qatar. The green line corresponds to diffuse ratios derived from Kt using the Erbs model. In spite of its relative simplicity, the model produces good results; however, deviations are seen at low and (especially) at high Kt when Kd is higher than expected. The blue and red lines represent models based on a polynomial (blue) and a polynomial with a Gaussian (red), which improve the agreement with observations. From GHI, these models derive DHI, and then DNI is obtained with Eq. 1. Figure 2 compares modelled and measured DNI, using the polynomial (left) and polynomial + Gaussian (right) models.

Fig.1: Measured 1-minute Kt and Kd for one year in Doha. The lines are the Erbs model (green), and two fitted functions: a polynomial (blue) and polynomial with Gaussian (red).

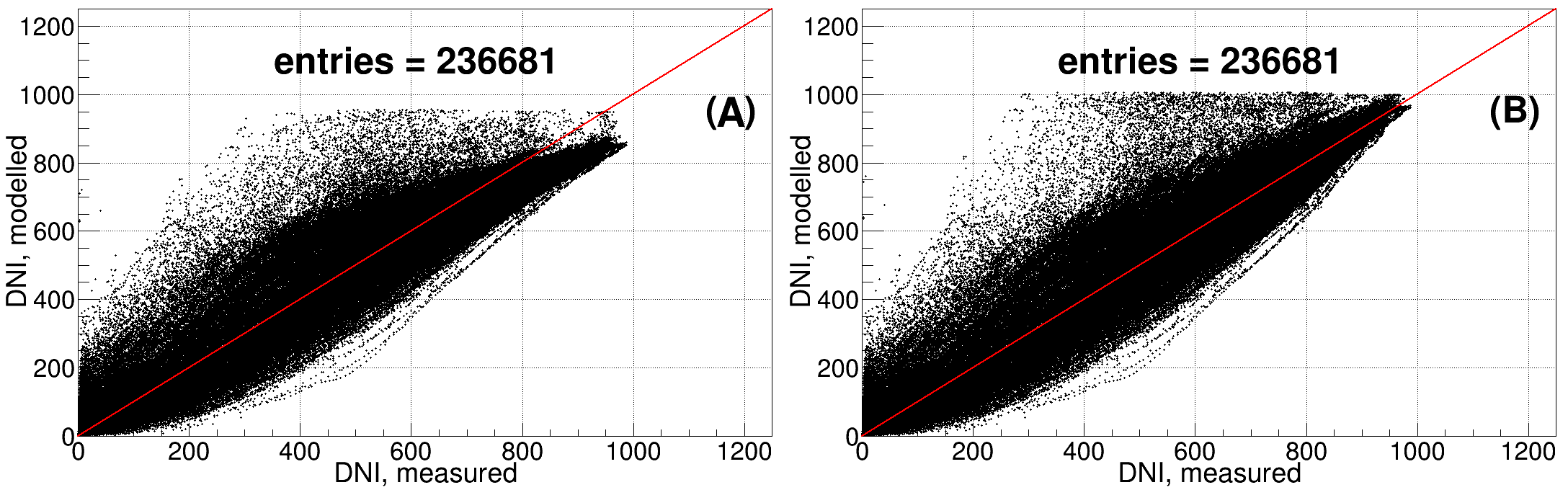
Fig.2: DNI as measured and derived from (a) polynomial and (b) polynomial + Gaussian models.